デシベル
無線がつながらないという問い合わせがあり、電波の強さを計測する機会がありました。そこでなんとなく使っていたデシベルという単位について、調べたことをまとめます。
ベル
デシベルはベルという単位に\dfrac{1}{10}を表す接頭辞d(デシ)がついたものです。デシリットルと同じですね。なので、デシベルを知るにはまずはベルを知ることになります。
1 [ベル] = 10 [デシベル]ベルは「AはBの100倍である」というような2つの値の比を表す相対的な単位です。単純な倍では桁数が大きくなり扱いにくい場合にベルが使われます。ベルは以下のように定義されています。
\text{ベル} = \log_{10} (2つの値の比) = \log_{10} \dfrac{\text{比較対象の値}}{\text{基準となる値}}比とベルの対照表は以下のようになります。1000000倍の場合、6ベルということになります。
| 比 | 計算式 | ベル |
|---|---|---|
| 1 | \log_{10} 1 = \log_{10} 10^0 | 0 |
| 2 | \log_{10} 2 | 0.301... |
| 5 | \log_{10} 5 | 0.699... |
| 10 | \log_{10} 10 | 1 |
| 50 | \log_{10} 50 = \log_{10} 5*10^1 = \log_{10} 5 + \log_{10} 10^1 | 1.699... |
| 100 | \log_{10} 100 = \log_{10} 10^2 | 2 |
| 500 | \log_{10} 500 = \log_{10} 5*10^2 = \log_{10} 5 + \log_{10} 10^2 | 2.699... |
| 1 000 | \log_{10} 1000 = \log_{10} 10^3 | 3 |
| 10 000 | \log_{10} 10000 = \log_{10} 10^4 | 4 |
| 100 000 | \log_{10} 100000 = \log_{10} 10^5 | 5 |
| 1 000 000 | \log_{10} 1000000 = \log_{10} 10^6 | 6 |
デシベル
実用上ではベルでは扱いにくいことがあります。例えば2倍はベルでは約0.3ベルということになり、小数点になってしまいます。そこでベルに \dfrac{1}{10}を表す接頭辞d(デシ)をつけたデシベル(dB)が多く使われます。1 [B] = 10 [dB] となるので、2倍は約3デシベルということになります。デシベルは以下のように定義されます。
\text{デシベル} = \mathbf{10} * \log_{10} \dfrac{\text{比較対象の値}}{\text{基準となる値}}音の強さとしてのデシベル
音の強さを表す単位としてデシベルが使われることがあります。このような画像や表を見たことはないでしょうか。
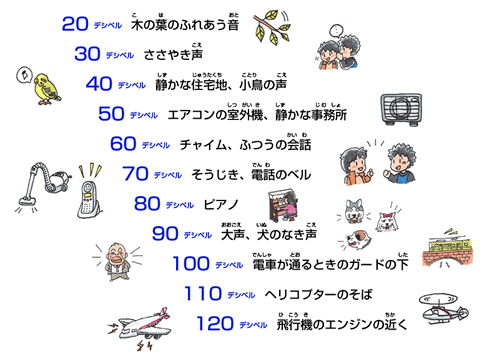
物理的に、音の強さは空気の圧力の変化量で決まります。単位はパスカル(Pa)です。人間がぎりぎり聞こえる音は20マイクロパスカル(20*10^{-6}パスカル)とされています。しかしジェット機のエンジン音などは200パスカルになります。また、圧力が倍になったら音の強さも倍になるわけではなく、圧力の2乗に比例すると言われています。
| 音 | 音の圧力 [Pa] | 音の強さ(音圧の2乗) | 比 |
|---|---|---|---|
| 人間がぎりぎり聞こえる音 | 0.000 02 | 0.000 000 000 4 | 1 (基準値) |
| ジェット機のエンジン音 | 200.000 00 | 40,000.000 000 000 0 | 100,000,000,000,000 |
人間がぎりぎり聞こえる音の強さを基準値とするとジェット機の音の強さは100,000,000,000,000倍なります。このような広い範囲を取る値にデシベルが便利なわけです。
人間がぎりぎり聞こえる音とされる20マイクロパスカルを基準としたときのデシベルを音圧レベルといいます。200パスカルの音圧レベルは、
10 * \log_{10} \dfrac{(200)^2}{(20*10^{-6})^2}
で表されます。
| 10 * \log_{10} \dfrac{(200)^2}{(20*10^{-6})^2} |
| \qquad = 10 * \log_{10} \left(\dfrac{200}{20*10^{-6}}\right)^2 |
| \qquad = 20 * \log_{10} \dfrac{200}{20*10^{-6}} |
| \qquad = 20 * \log_{10} \dfrac{\cancel{2}*10^2}{\cancel{2}*10^{-5}} |
| \qquad = 20 * \log_{10} 10^7 |
| \qquad = 140 [\mathrm{dB}] |
| 音 | 音の強さ(音圧の2乗) | 比 | デシベル |
|---|---|---|---|
| 人間がぎりぎり聞こえる音 | 0.000 000 000 4 | 1 (基準値) | 0 (基準値) |
| ジェット機のエンジン音 | 40,000.000 000 000 0 | 100,000,000,000,000 | 140 |
利得としてのデシベル
利得とは「入力と出力の比」のことで、装置を通す前と後を比べて値がどれだけ増えた(減った)かということです。
■問1■ ある増幅装置の入力に5を与えたところ、200の出力が得られました。この増幅装置の利得は何デシベルでしょうか。

入力を基準としてベルの値を求めれば良いので、
| 10 * \log_{10} \dfrac{\mathrm{出力}}{\mathrm{入力}} |
| \qquad = 10 * \log_{10} \dfrac{200}{5} |
| \qquad = 10 * \log_{10} 40 |
| \qquad = 10 * \log_{10} (4*10) |
| \qquad = 10 * (\log_{10} 4 + \log_{10} 10) |
| \qquad \fallingdotseq 10 * ( 0.602 + 1) |
| \qquad \fallingdotseq 16 [\mathrm{dB}] |
以上から「この増幅装置の利得は16デシベルである」ことになります。これは「この増幅装置は入力の40倍(=10^{16/10})の出力が得られる」というのと同義です。
■問2■ 利得が8デシベルの増幅装置を5段重ねました。入力として1*10^{-6}を与えたときの出力は何でしょうか。

1つの増幅装置の利得は8[デシベル]のとき、5段重ねたときの利得は 8+8+8+8+8 = 40 [デシベル]です。実際の比は 10^{ベル} = 10^{デシベル/10}で求められるので、 10^{40/10} = 10^4倍となります。
入力が1*10^{-6} のときの出力は
1*10^{-6} * 10^4 = 0.01
となります。
これをベルを使わずに計算してみます。
1つの増幅装置の利得は 8[デシベル] \fallingdotseq 6.3096 [倍]になるので、5段重ねたときの出力は入力の約 6.3096 * 6.3096 * 6.3096 * 6.3096 * 6.3096 \fallingdotseq 10,000.2 [倍]になります。なので入力が 1*10^{-6} のときの出力は
1 * 10^{-6} * 10000.2 \fallingdotseq 0.01 [V]
となります。
負のデシベル
デシベルは負の値になることがあります。
■問3■ とある減衰装置の入力に4000を与えたところ、0.0016の出力が得られました。 この減衰装置の利得は何デシベルでしょうか。
問1と同じように入力を基準として、デシベルを求めます。
| 10 * \log_{10} \dfrac{\mathrm{出力}}{\mathrm{入力}} |
| \qquad = 10\log_{10} \dfrac{0.0016}{4000} |
| \qquad = 10\log_{10} \dfrac{16*10^{-4}}{4*10^3} |
| \qquad = 10\log_{10} \dfrac{4}{10^7} |
| \qquad = 10 * (\log_{10} 4 - \log_{10} 10^7) |
| \qquad \fallingdotseq 10 * ( 0.602 - 7) |
| \qquad \fallingdotseq -64 [\mathrm{dB}] |
以上から「この減衰装置の利得は-64デシベルである」ということになります。これは「この減衰装置は入力の10^{-64/10}倍の出力が得られる」というのと同じです。検算してみましょう。
4000 * 10 ^{(-64/10)} = 0.00159242\dots \fallingdotseq 0.00159このように基準となる値より比較対象の値が小さい場合、デシベルの値は負になります。
| 比 | デシベル |
|---|---|
| 0.000 001 | -60 |
| 0.000 01 | -50 |
| 0.000 1 | -40 |
| 0.001 | -30 |
| 0.005 | -23.01... |
| 0.01 | -20 |
| 0.05 | -13.01... |
| 0.1 | -10 |
| 0.5 | -3.01... |
| 1 | 0 |
| 2 | 3.01... |
| 5 | 6.99... |
| 10 | 10 |
| 50 | 16.99... |
| 100 | 20 |
| 500 | 26.99... |
| 1 000 | 30 |
| 10 000 | 40 |
| 100 000 | 50 |
| 1 000 000 | 60 |
電波の強さとしてのデシベル
電波の強さの指標はいくつかありますが、かんたんに計測できるものとして受信電力があります。受信電力はワット(W)で表されます。無線で使われる電波は非常に弱く、幅が広いです。1μW(10^{-6} [W])から100nW( 10^{-7} [W])あれば安定した無線通信ができるとされており、1nW(10^{-9} [W])を下回ると不安定になると言われています。
無線の電波の強さをデシベルで表すときには、1mWを基準値としてデシベルを計算します。
| 受信電力 | デシベル | デシベルの計算式 |
|---|---|---|
| 1μW(10^{-6} [W]) | -30 | 10 \log_{10}\dfrac{10^{-6}}{10^{-3}} = 10 \log_{10} 10^{-3} |
| 100nW( 10^{-7} [W]) | -40 | 10 \log_{10}\dfrac{10^{-7}}{10^{-3}} = 10 \log_{10} 10^{-4} |
| 1nW(10^{-9} [W]) | -60 | 10 \log_{10}\dfrac{10^{-9}}{10^{-3}} = 10 \log_{10} 10^{-6} |
この結果を踏まえて、デシベルで1段落目を書き直してみます。
電波の強さを表す単位はいくつかありますが、受信電力はワット(W)で表すことができます。無線で使われる電波は非常に弱く、幅が広いです。1mWを基準として-30dBから-40dBあれば安定した無線通信ができるとされており、-60dBを下回ると不安定になると言われています。
だいぶ扱いやすい数字になりましたね。
この1mWを基準値としたデシベルは、RSSI(Received Signal Strength Indicator、直訳:受信信号強度指標)と呼ばれ、dBmという単位を使用します。単位についているmはmWのmのことで、ディービーエムと読みます。デシベルエムなどとは読みません。
受信品質としてのデシベル
電波には受信したい信号(シグナル)だけでなく背景雑音(ノイズ)があります。シグナルとノイズのdBmをそれぞれ計算したとき、シグナルの強度とノイズの強度の差を信号対雑音比(SNR、SN比)と呼びます。単位はdBです。
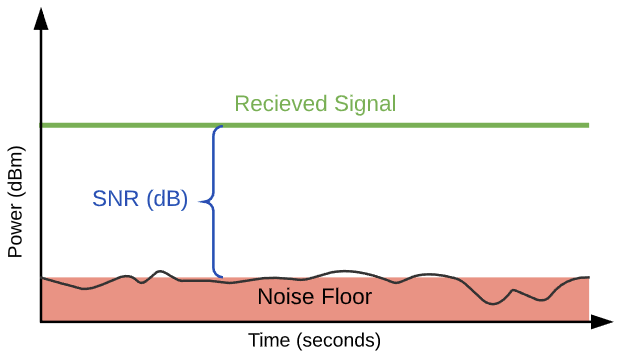
シグナルが-30dBm、ノイズが-90dBmの場合、SNRは-30 - (-90) = 60[\mathrm{dB}]となります。
Wireless-Nets, Ltd.によると、SNR値によって実際の通信状況は以下のようになるとされています。
| SNR | 通信状況 |
|---|---|
| 40dB~ | 非常に良い |
| 25dB~40dB | とても良い |
| 15dB~25dB | やや悪い |
| 10dB~15dB | 悪い |
| 5dB~10dB | 通信できない |
Ciscoによると、データ通信であれば20dB以上、音声通信であれば25dB以上のSNRが推奨されています。
絶対値を表すデシベル
デシベルの定義はある基準と比べての大きさを表すもので相対的な値です。ですが基準を一つに定めると絶対値を表す単位として使うことができます。本記事の音の大きさとしてのデシベルや電波の強さとしてのデシベルは、それぞれ基準が決められているので絶対値を表す単位になっています。
2乗値のデシベル
デシベルの計算式で以下のように20が掛けられていることがあります。
デシベル = \mathbf{20} * \log_{10} \dfrac{比較対象の値}{基準となる値}これは音圧レベルのように2乗した値を比較するときに、予め2乗を計算しておいたものです。
| 音 | 音圧 [Pa] | 音の強さ(音圧の2乗) |
|---|---|---|
| 基準 | A | A^2 |
| 比較対象 | B | B^2 |
| 10 * \log_{10} \dfrac{\mathrm{比較対象の値}}{\mathrm{基準となる値}} |
| \qquad = 10 \log_{10} \dfrac{B^2}{A^2} |
| \qquad = 10 \log_{10} \left(\dfrac{B}{A}\right)^2 |
| \qquad = 20 \log_{10} \dfrac{B}{A} |
こうすることで2乗を計算しなくてよくなります。ジェット機のエンジン音をこの式を用いて計算してみましょう。「音の強さとしてのデシベル」の項で計算したときより楽に計算できます。
| 音 | 音圧 [Pa] |
|---|---|
| 人間がぎりぎり聞こえる音 | 0.000 02 |
| ジェット機のエンジン音 | 200.000 00 |
| 20 * \log_{10} \dfrac{200}{0.00002} |
| \qquad = 20 * \log_{10} \dfrac{20000000}{2} |
| \qquad = 20 * \log_{10} 10^7 |
| \qquad = 140 [\mathrm{dB}] |
2乗値の場合、比から出力や入力を計算するときも注意が必要です。
\dfrac{比較対象の値}{基準となる値} = X [倍]ここでこれらの値が2乗であった場合、
\dfrac{(元の比較対象の値)^2}{(元の基準となる値)^2} = X[倍]なので
\sqrt{\dfrac{(元の比較対象の値)^2}{(元の基準となる値)^2}} = \sqrt{X} [倍] \quad \Rightarrow \quad \dfrac{元の比較対象の値}{元の基準となる値} = \sqrt{X} [倍]となり、平方根を取る必要があります。
■問4■ ジェット機のエンジン音は音圧レベルは140[dB]です。このとき、ジェット機のエンジン音の音圧は何[Pa]でしょうか。ただし、音圧レベルとは音圧の2乗値の比であり、基準となる音圧は0.00002[Pa]です。
ここで、140[dB]ということは10^{14}倍ということですが、あくまで音圧の2乗値が10^{14}倍なので、音圧自体は\sqrt{10^{14}}=10^7倍になります。
なので 0.00002 * \sqrt{10^{14}} = 200 [\mathrm{Pa}]となります。
| 基準となる音 | ジェット機のエンジン音 (比較対象の値) | ||
|---|---|---|---|
| 音圧 [Pa] | 0.000 02 \left(\sqrt{0.000 000 000 4}\right) | → \left(\sqrt{10^{14}}倍\right) | 200 \left(\sqrt{40000}\right) |
| 音の強さ (音圧の2乗に比例) | 0.000 000 000 4 | → \left(10^{14}倍\right) | 40000 |
参考文献
- ONO SOKKI Co., Ltd.: 騒音計とは
- Shimamura Music: dB(デシベル)って何?音圧とは?
- Cisco Systems: 無線の基礎:信号対雑音比(SNR)と無線信号強度
- Wireless-Nets, Ltd.: How to: Define Minimum SNR Values for Signal Coverage
- BUFFALO INC.: よくあるご質問 無線環境が安定するRSSI強度はどの程度ですか?
